Definitions and Calculations of Step Lengths
In literature there are many different definitions of step length. In the following three approaches to define and compute step lengths are defined.
Side specific step lengths
In the first and second experiment the step lengths are defined side specific to both left and right foot. Therefore the absolute distance l1 of the left heel positions between two ground touches of the left foot are computed. The same is done for the absolute distance r2 of the right foot.

A similar approach is described in Figure 3.2 in Schepers, Martin: Ambulatory Assessment of Human Body Kinematics and Kinetics, University of Twente, PHD Thesis, 2009, See on XSense.com.
Alternative 1: Using Regression on walking path
Step lengths also could be defined as the horizontal distance s between the left and the right heel along the plane of motion progress.
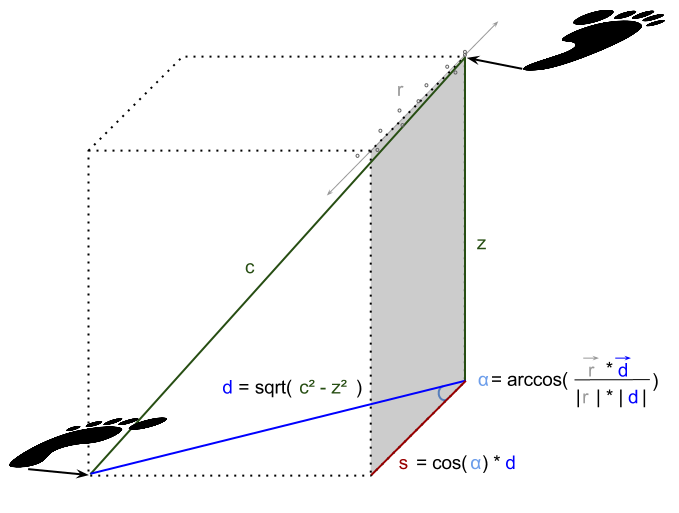
As shown in the figure below the direct connection between the 3D position data d and a direction vector r is used to approximate the step length s. The direction vector r could be extracted using linear regression on the X- and Y-values of the position data of one foot.
Alternative 2: Using angular extend of legs
A second approach to calculate step length would be to define the step length as the horizontal distance between left and right heel along the plane of motion progress.
To get the horizontal plane distance s it is possible to approximate the step length by observing the angular extent between the legs during a swing phase. To compute the distance s it is possible to use the following approximation for a proband with leg height h. Maximal angular extend can be considered as a criterion that both feet are standing on the ground. So to calculate step lengths the distances s could be used for all maximal angular extents.

This definition is taken from Moore, Steven T. ; MacDougall, Hamish G. ; Gracies, Jean-Michel ; Cohen, Helen S. ; Ondo, William G.: Long-term monitoring of gait in Parkinson’s disease. In: Gait & posture 26 (2007), Juli, Nr. 2, S. 200-7. - ISSN 0966-6362 See PubMed.
Extraction and Computation of Step Lengths
In the implementation of calcStepLength the side specific definition of step length is used. Therefore the step phases (when a foot is touching the ground) need to be recognized. During a step phase one foot is standing on the ground, the other foot is moving and passing over. So the following three criteria are used to define a part of a step phase:
Step phase criteria
- The velocity of the standing foot is smaller than an computed or adapted ε-threshold (considering small movements like the rolling motion of a foot).
- The velocity of the moving foot is larger than an computed or adapted ε-threshold.
- The absolute distance between the left and the right heel is smaller than a computed or adapted distance-ε-threshold.
Velocities criteria and ε-threshold
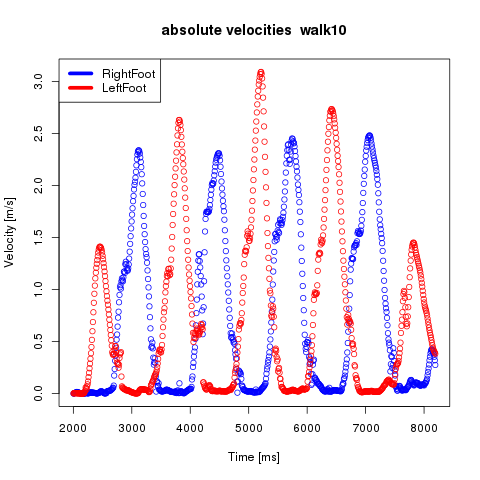
The following picture shows the absolute velocity process for left and right foot (heels) during a time span of five seconds of a natural walk in a straight corridor.
Original call: ./calcStepLength --inputfile="../experiments/experiment1/walk10.mvnx" --outputdir="online/images/diagrams/walk10/" --segments="LeftFoot, RightFoot" --format="png" --title="walk10" --min="2000" --max="8200" --colors="blue, red, green, cyan, orange, darkblue, darkred"
A peak of the absolute velocity progress for a foot characterises the correspondent swing phase. The time spans in which the absolute velocity is close to zero respectively smaller than a computed or well chosen ε-threshold point to a standing phase of a foot. In this context well chosen means considering small movements like the rolling motion of a foot. Time Spans in which additionally the other foot is moving (meaning it has a velocity larger than the ε-threshold) are indicating that a step is taking place and is confirmed with the third criteria (small distance). It is important to choose the ε-threshold big enough to ingore rolling motions and obviously small enough considering the maximal motion velocity of a foot.
The absolute distance criterion
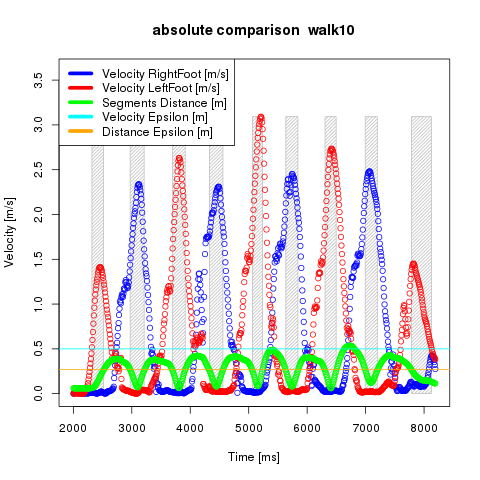
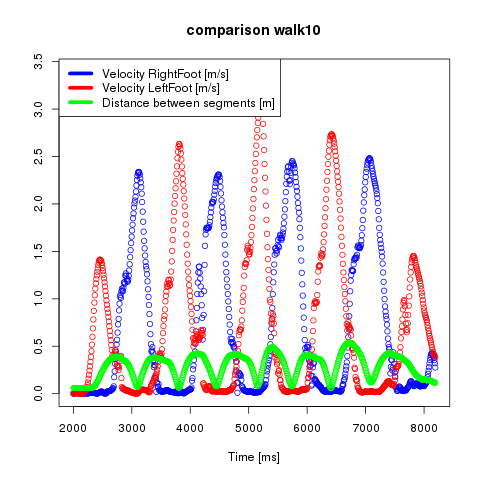
Additionally only times for step phases are considered in which the absolute distance between the both heels is minimal, respectively below a distance-ε-threshold. In the following figure the progression of the absolute distance beside the absolute velocities is shown.
Original call: ./calcStepLength --inputfile="../experiments/experiment1/walk10.mvnx" --outputdir="online/images/diagrams/walk10/" --segments="LeftFoot, RightFoot" --format="png" --title="walk10" --min="2000" --max="8200" --colors="blue, red, green, cyan, orange, darkblue, darkred"
The swing phase when the moving foot passes the standing foot is characterised through a local minimum of the absolute distance between the two feet. Accordingly the median of all absolute distances is used as an additional distance-6#949;-threshold. This allows to narrow down the time spans used to identify the standing phases of a foot.
Filtering and Computing
In the following figure the grey boxes are representing the time spans in which all three criteria are fulfilled. Beside the time spans the diagram shows both velocity and distance ε-thresholds as horizontal lines.
Original call: ./calcStepLength --inputfile="../experiments/experiment1/walk10.mvnx" --outputdir="online/images/diagrams/walk10/" --format="png" --title="walk10" --colors="blue, red, green, cyan, orange, darkblue, darkred" --min="2000" --max="8200" --velepsilon="0.5"
To calculate the foot specific step length the lowest heel position of every step phase time span (in which all criteria are fulfilled) is used. Accordingly to compute the step lengths the corresponding absolute euclidian distances between these lowest positions for every successive step phases are used.